A absorção de radiação infravermelha deve ser tanto maior quanto maior for a variação do momento dipolar da molécula durante a vibração. Mediante um tratamento mecânico-quântico, pode ser deduzido que a intensidade integrada de uma banda de absorção no espectro infravermelho é proporcional ao quadrado da derivada do momento dipolar em relação à distância de ligação, nas proximidades da região de equilíbrio. Esta derivada é de difícil acesso, de modo que não se pode predizer, teoricamente, a intensidade da banda. Todavia, a experiência tem mostrado que quando o momento dipolar da ligação é grande, a banda costuma ser de grande intensidade e vice-versa. Assim, pode-se estimar a intensidade das bandas tendo-se em conta a grandeza do momento dipolar, que depende, principalmente, da diferença de eletronegatividade dos átomos envolvidos na ligação.

Uma molécula diatômica pode considerar-se aproximadamente como um oscilador harmônico, cujos átomos efetuam vibrações periódicas com uma freqüência ou número de onda dado pela equação:

Em moléculas heteronucleares, como por exemplo, HF, HCl, CO, etc., o momento dipolar oscila com a mesma freqüência da vibração, por que segundo a eletrodinâmica clássica, podem absorver radiação infravermelha, dando lugar a uma banda fundamental de absorção, cujo número de ondas é dado pela equação 6. Segundo a mecânica clássica, a força é a derivada, com sinal trocado, da energia potencial V respeito a distância r, tendo em conta que a força é:

resulta que:

A representação gráfica de V em função de r é portanto uma parábola, com vértice V = 0, isto é, quando a distância é a de equilíbrio entre os átomos, como pode ser visto na FIGURA 2.

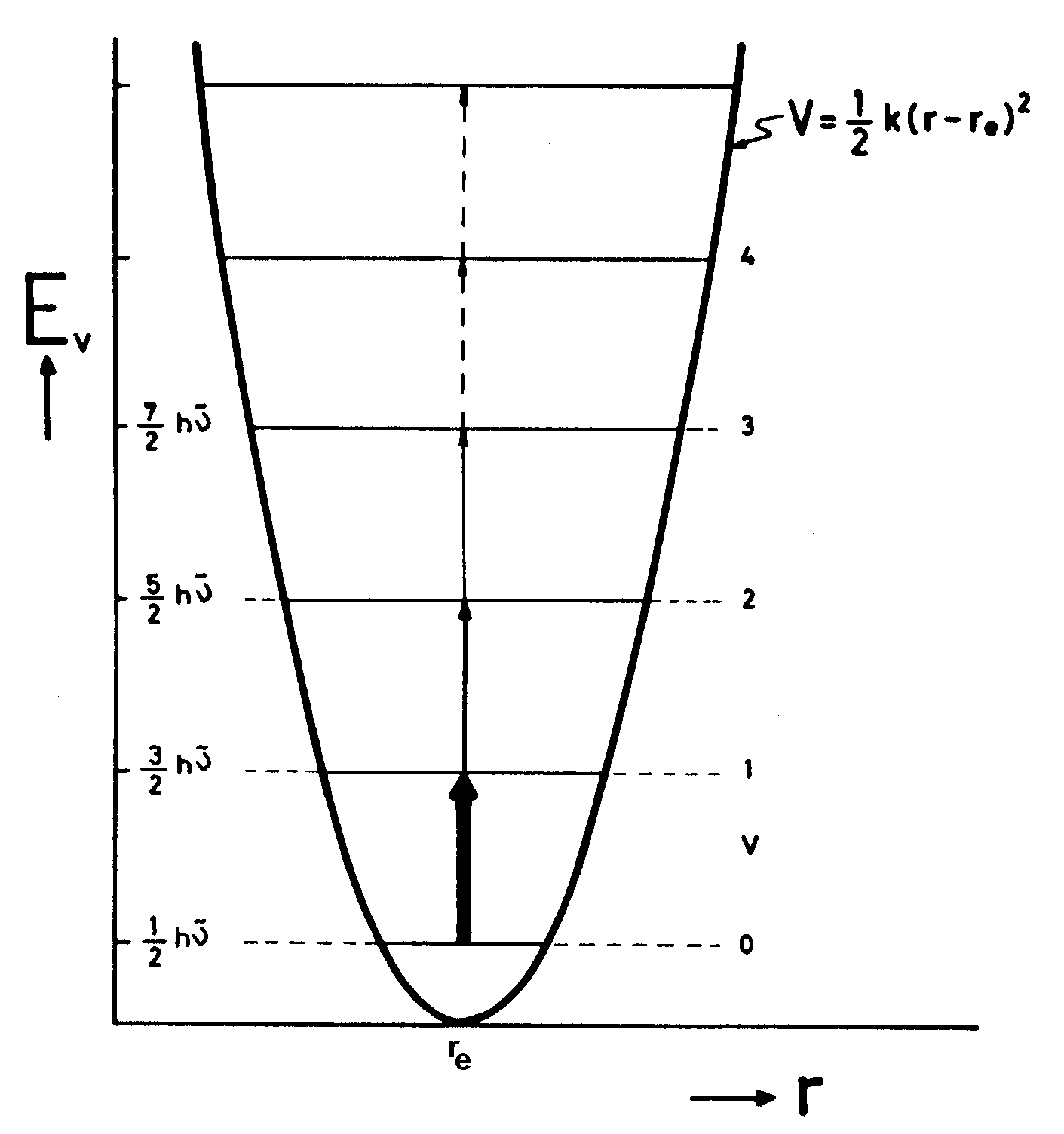
FIGURA 2 - Curva de Energia Potencial para as Vibrações Harmônicas
de uma Molécula Diatômica.

anterior

próxima

principal