
TCC aplicada à complexos tetraédricos
A Teoria do Campo Cristalino pode ser
aplicada também à complexos tetraédricos, neste caso o
desdobramento dos orbitais atômicos do íon metálico será
feito de uma forma diferente, na verdade, de forma inversa ao que
ocorre para complexos octaédricos.
No caso da geometria tetraédrica, os ligantes se aproximarão do
íon metálico, segundo as diagonais, ou seja, os orbitais do
íon metálico que sofrerão mais serão os orbitais que não
estão dispostos ao longo do eixo de coordenadas, ou seja, os
orbitais, dxy, dxz, dyz, com
isso, estes orbitais serão desestabilizados em 4 Dq e os
orbitais dx2 - y2 e o dz2 serão
estabilizados de 6 Dq, pois eles não estão participando
diretamente da ligação.

Faça a distribuição dos elétrons para a geometria tetraédrica
10 Dq tetraédrico = 4/9 . 10 Dqoctaédrico
Para complexos tetraédricos, só é possível que eles sejam spin alto.
Existem complexos de metais de transição
com ligantes volumosos e configuração eletrônica d0
, d5, d10, que são tetraédricos, nestes
casos a EECC = 0.
Caso o complexo de metal de transição possua número de
coordenação igual à 4 e seja spin baixo, então este complexo
será quadratico plano e os orbitais atômicos do íon metálico
serão distribuídos da mesma forma que na geometria octaédrica.
Distorções
tetragonais da geometria octaédrica
As distorções tetragonais são, na verdade, alongamentos e compressões das ligações dos ligantes axiais, ou seja todas as distância das ligações M-L do complexo são do mesmo tamanho, exceto as ligações axiais, que podem ser maiores ou menores.
alongamento |
 compressão |
As distorções tetragonais são
favorecidas na presença do efeito Jahn - Teller , que afirma
que: "qualquer molécula não linear, em um estado
eletrônico degenerado, sofrerá distorções, para remover a
degenerescência e diminuir a energia do sistema."

Alongamento dos ligantes ao longo do eixo z.
Maior afastamento e estabilização dos orbitais z.
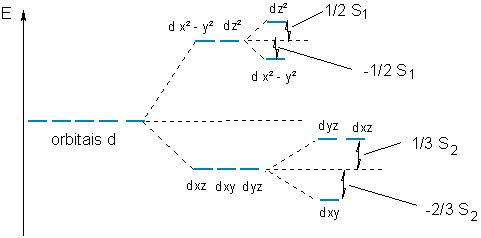
Compressão dos ligantes ao longo do eixo z.
Maior interação dos orbitais z, maior energia dos mesmos.
O caso da geometria quadrático plano é um caso especial de distorção tetragonal, considerando que o afastamento dos ligantes ao longo do eixo z foram feitos para o infinito.