TCC Aplicada à Complexos Quadráticos Planos

A TCC, além de explicar complexos octaédricos e tetraédricos também explica complexos quadráticos planos.
A geometria quadrática plana é considerada como um caso especial de distorção tetragonal, onde os ligantes axiais são distanciados ao infinito, ou seja, eles são removidos do sistema de coordenação do complexo. Com este distanciamento dos ligantes ao longo do eixo z, os orbitais que contém a componente z serão bastante estabilizados.
Quando temos este caso, os ligantes que provocam um maior desdobramento do campo, ou seja, os ligantes de campo forte serão favorecidos, ou seja, os complexos que possuem ligantes de campo forte e número de coordenação igual a 4, terão preferência em se organizar com a geometria quadrático plano.

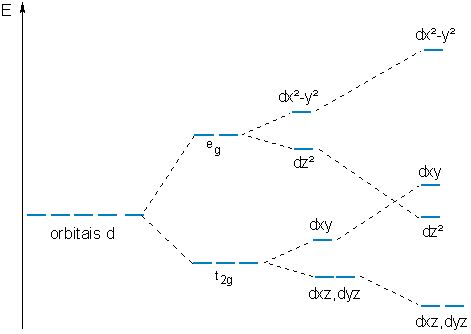
desdobramento dos orbitais d para complexos quadráticos planos

A partir do desdobramento dos orbitais, é possível notar que ocorre uma grande estabilização dos orbitais que contém as coordenadas z. O orbital dx² - y² é o mais energético, pois ele está ao longo dos eixos x e y, pois os ligantes se aproximam através destes eixos.
O preenchimento dos orbitais ocorrem de tal forma que o orbital dx² - y² não são preenchidos.
Como foi dito esta geometria é favorável para complexos com ligantes campo forte, sendo assim o complexo será spin baixo, não ocorrendo complexos spin alto.
Os complexos spin alto e de número de coordenação igual a 4, são de geometria tetraédrica.
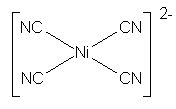
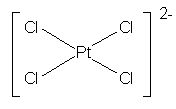
Exemplos de complexos com geometria quadrática plana são [Ni(CN)₄]^2-, [PtCl₄]^2- .

principal